Soal Persamaan dan Pertidaksamaan Rasional dan Irasional

1.) Nilai $x$yang memenuhi persamaan $\sqrt{17x-\sqrt{x^2-5}}=7$ adalah $\cdots \cdot$
A. $x=-3$                      D. $x=9$
B. $x=3$                          E. $x=49$
C. $x=5$

Pembahasan

Diketahui $\sqrt{17x-\sqrt{x^2-5}}=7$.

Kuadratkan kedua ruas, lalu sederhanakan sampai diperoleh bentuk akar tunggal dalam satu ruas.

$\begin{array}{cc}(\sqrt{17x-\sqrt{x^2-5}}{)}^2& =7^2\\ 17x-\sqrt{x^2-5}& =49\\ -\sqrt{x^2-5}& =49-17x\\ \sqrt{x^2-5}& =17x-49\end{array}$

Kuadratkan kedua ruas lagi, lalu selesaikan.

$$\begin{array}{cc}(\sqrt{x^2-5}{)}^2& =(17x-49{)}^2\\ x^2-5& =289x^2-1.666x+2.401\\ 288x^2-1.666x+2.406& =0\\ 144x^2-833x+1.203& =0\\ (144x-401)(x-3)& =0\end{array}$$Diperoleh $x=\frac{401}{144}$ atau $x=3$

Syarat akar:
$17x-49\ge 0\iff x\ge \frac{49}{17}$

Perhatikan bahwa $x=3$ memenuhi syarat akar ini, tetapi tidak untuk $x=\frac{401}{144}$.
Uji nilai $x=3$ pada persamaan mula-mula.
$\begin{array}{cc}\sqrt{17x-\sqrt{x^2-5}}& =7\\ \Rightarrow \sqrt{17\left(3\right)-\sqrt{3^2-5}}& =7\\ \sqrt{51-\sqrt{4}}& =7\\ \sqrt{49}& =7\end{array}$
Jadi, nilai $x=3$ merupakan penyelesaian persamaan tersebut.
(Jawaban B)

2.)Tentukan himpunan penyelesaian dari pertidaksamaan irasional √ x – 5   < 2

A. x > 9

B. x < 9

C. x = 10

D. x = 9

E. x > 10

Penyelesaian soal

Untuk menjawab soal ini kita tentukan terlebih dahulu syarat agar pertidaksamaan irasional berlaku yaitu:

x – 5 ≥ 0

x ≥ 5

Selanjutnya kita kuadratkan kedua ruas pertidaksamaan irasional sehingga didapat:

(√ x – 5 )2 < 22.

x – 5 < 4

x < 4 + 5 atau x < 9

(Jawaban B)

3.) Tentukan nilai x yang memenuhi persamaan rasional x–1 /2 – 3x/4 = 0

A. 2               C. -2        E. = 5

B. -3              D. 3

Penyelesaian soal

Untuk menjawab soal ini kita gunakan metode pindah ruas dan kali silang. Ketika memindahkan angka atau variabel dari satu ruas ke ruas lainnya kita ganda negatif menjadi positif atau sebaliknya. Jadi jawaban soal diatas sebagai berikut:

→ x–1 /2 = 3x /4

 → 4 (x – 1) = 2. 3x 

→ 4x – 4 = 6x 

→ 4x – 6x = 4 

→ -2x = 4 

→ x = -4/2 = -2

(Jawaban C)

4.) Penyelesaian √2x+6>0 adalah ⋯⋅

A. x<3                              D. x>−3
B. x≤−3                           E. x>6
C. x≥−3 

Pembahasan

Diketahui √2x+6>0.
Kuadratkan kedua ruas, lalu selesaikan.
(√2x+6)2>(0)22x+6>02x>−6x>−3

Syarat akar:
2x+6≥0⇔x≥−3
Karena semua x yang memenuhi x>−3 juga memenuhi syarat akar x≥−3, maka penyelesaian pertidaksamaan tersebut adalah x>−3

(Jawaban D)

5.) Jika √3x−1<2, maka nilai x yang memenuhipertidaksamaan tersebut adalah ⋯⋅

A. x<53                          D. 13<x<53
B. x>13                          E. 13<x≤53
C. 13≤x<53

Pembahasan

Diketahui √3x−1<2.
Kuadratkan kedua ruas, lalu selesaikan.
(√3x−1)2<(2)23x−1<43x<5x<53(★)
Syarat akar:
3x−1≥0⇔x≥13
Gunakan garis bilangan.

Irisan dari ★ dan syarat akar di atas merupakan penyelesaian pertidaksamaan.
Tampak bahwa irisan dari (1) dan (2) adalah 13≤x<53
(Jawaban C)

6.) Jika $\sqrt{3-5x}>\sqrt{x}$, maka nilai $x$ yang memenuhi adalah $\cdots \cdot$

A. $x\ge 0$                              B. $0\le x<\frac{1}{2}$
C. $x<\frac{1}{2}$                        D. $\frac{1}{2}\le x<\frac{3}{5}$
E. $x\le \frac{3}{5}$

Pembahasan

Diketahui $\sqrt{3-5x}>\sqrt{x}$.
Kuadratkan kedua ruas, lalu selesaikan.
$\begin{array}{cccc}(\sqrt{3-5x}{)}^2& >(\sqrt{x}{)}^2& & \\ 3-5x& >x& & \\ -6x& >-3& & \\ x& <\frac{1}{2}& & \left(★\right)\end{array}$

Syarat akar $(1)$:

$3-5x\ge 0\iff x\le \frac{3}{5}$
Syarat akar $\left(2\right)$: $x\ge 0$.
Gunakan garis bilangan.
Irisan dari $\left(★\right)$ dan kedua syarat akar di atas merupakan penyelesaian pertidaksamaan.

Tampak bahwa irisannya adalah $0\le x<\frac{1}{2}$
(Jawaban B)

7.) Himpunan penyelesaian $\sqrt{x^2-3x+2}\le \sqrt{x+7}$ adalah $\cdots \cdot$

A. $\{x|x\ge 5,x\in R\}$
B. $\{x|-1\le x\le 5,x\in R\}$
C. $\{x|-7\le x\le 7\text{atau}2\le x\le 5,x\in R\}$
D. $\{x|-1\le x\le 1\text{atau}2\le x\le 5,x\in R\}$
E. $\{x|-1\le x<0\text{atau}2\le x\le 5,x\in R\}$

Pembahasan

Diketahui $\sqrt{x^2-3x+2}\le \sqrt{x+7}$.
Kuadratkan kedua ruas, lalu selesaikan.
$\begin{array}{cc}(\sqrt{x^2-3x+2}{)}^2& \le (\sqrt{x+7}{)}^2\\ x^2-3x+2& \le x+7\\ x^2-4x-5& \le 0\\ (x+1)(x-5)& \le 0\end{array}$
Pembuat nol: $x=-1$ atau $x=5$.
Penyelesaiannya adalah $-1\le x\le 5(\mathrm{★)}$

Syarat akar $(1)$:

$x^2-3x+2\ge 0\iff (x-1)(x-2)\ge 0$
Pembuat nol: $x=1$ atau $x=2$.
Penyelesaiannya adalah $x\le 1\text{atau}x\ge 2$.

Syarat akar $(2)$:
$x+7\ge 0\iff x\ge -7$
Gunakan garis bilangan.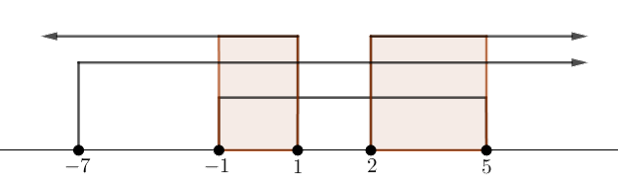

Irisan dari $★$ dan kedua syarat akar di atas merupakan himpunan penyelesaian pertidaksamaan.

Tampak bahwa irisannya adalah irisannya adalah 

$\boxed{{\displaystyle \{x|-1\le x\le 1\text{atau}2\le x\le 5,x\in \mathbb{R}\}}}$
(Jawaban D)

8.)Jika pertidaksamaan $\sqrt{3-ax}\le 2$ dipenuhi oleh interval $a-2\le x\le 3$, maka nilai $a^2-a=\cdots \cdot$

A. $4$                      C. $2$                  E. $0$
B. $3$                      D. $1$          

Pembahasan

Diketahui $\sqrt{3-ax}\le 2$.
Kuadratkan kedua ruas untuk memperoleh $3-ax\le 4$.
Syarat akar: $3-ax\ge 0$.
Dari sini, kita peroleh
$\begin{array}{cc}& 0\le 3-ax\le 4\\ & -3\le -ax\le 1\\ & -\frac{1}{a}\le x\le \frac{3}{a}\end{array}$
Karena diketahui bahwa pertidaksamaan $\sqrt{3-ax}\le 2$ 

terpenuhi oleh interval $a-2\le x\le 3$, maka jelas bahwa $a=1$.

Dengan demikian, nilai dari $a^2-a=(1{)}^2-1=0$

(Jawaban E)

9.) Sebuah sepeda melaju di jalan raya selama $t$ jam dengan lintasan tempuh (dalam satuan kilometer) ditentukan oleh persamaan $S\left(t\right)=\sqrt{t^2-10t+40}$ dan panjang lintasan yang ditempuh sekurang-kurangnya $10$ km. Bentukpertidaksamaan yang menyatakan masalah di atas adalah $\cdots \cdot$

A. $\sqrt{t^2-10t+40}>10$
B. $\sqrt{t^2-10t+40}\ge 10$
C. $\sqrt{t^2-10t+40}<10$
D. $\sqrt{t^2-10t+40}\le 10$
E. $\sqrt{t^2-10t+40}>0$

Pembahasan

Karena $S\left(t\right)$ menyatakan jarak tempuh dan panjang lintasan yang ditempuh (jarak) sekurang-kurangnya $10$ km, yang dalam hal ini diartikan juga sebagai PALING SEDIKIT (PALING PENDEK) $10$ km, maka tanda yang digunakan adalah $\ge$.
Jadi, pertidaksamaan yang tepat adalah $\sqrt{t^2-10t+40}\ge 10$
(Jawaban B)

10.) Jika $x>\sqrt{x+12}$, nilai $x$ yang memenuhi adalah $\cdots \cdot$

A. $-12<x<-3$ atau $x>4$             
B. $x<-3$ atau $x>4$                         
C. $x<-12$
D. $x>0$
E. $x>4$

Pembahasan

Diketahui $x>\sqrt{x+12}$.
Ruas kiri pada pertidaksamaan di atas belum tentu bernilai non-negatif. Oleh karena itu, perlu diuraikan menjadi dua kemungkinan, yaitu $x<0$ dan $x\ge 0$.

Kasus 1: $x<0$
Oleh karena $\sqrt{x+12}\ge 0$ dan $x<0$, maka $x>\sqrt{x+12}$ tidak akan memiliki penyelesaian untuk setiap $\mathrm{x.}$

Kasus 2: $x\ge 0$
Oleh karena $x\ge 0$, maka kedua ruas padapertidaksamaan tersebut tidak bernilai negatif sehingga boleh dikuadratkan.
Kuadratkan kedua ruas, lalu selesaikan.
$\begin{array}{cc}(x{)}^2& >(\sqrt{x+12}{)}^2\\ x^2& >x+12\\ x^2-x-12& >0\\ (x+3)(x-4)& >0\end{array}$
Pembuat nol: $x=-3$ atau $x=4$.
Penyelesaiannya adalah $x<-3\text{atau}x>4\left(★\right)$
Syarat akar $(1)$: $x\ge 0$
Syarat akar $(2)$:
$x+12\ge 0\iff x\ge -12$
Gunakan garis bilangan.

Irisan dari $★$ dan kedua syarat akar di atas merupakan himpunan penyelesaianpertidaksamaan.
Tampak bahwa irisannya adalah $\boxed{{\displaystyle x>4}}$
(Jawaban E)

11.)  Nilai $x$ yang memenuhi pertidaksamaan $\sqrt{x-3}>5-x$ adalah $\cdots \cdot$

A. $4<x<7$                             D. $x>4$
B. $4<x<5$                             E. $x\ge 4$
C. $3\le x\le 5$

Pembahasan

Diketahui $\sqrt{x-3}>5-x$.
Ruas kanan pada pertidaksamaan di atas belum tentu bernilai positif. Oleh karena itu, perlu diuraikan menjadi dua kemungkinan, yaitu $5-x<0$ dan $5-x\ge 0$.
Kasus 1: $5-x<0⟺x>5$
Oleh karena $\sqrt{x-3}\ge 0$ dan $x>5$, maka $\sqrt{x-3}>5-x$ terpenuhi untuk semua $x$.
Syarat akar: $x-3\ge 0⟺x\ge 3$.
Irisan dari $x>5,x\in R$, dan $x\ge 3$direpresentasikan oleh garis bilangan berikut.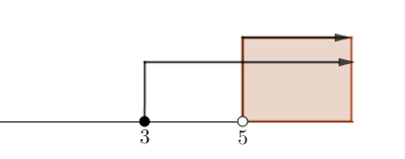

Penyelesaiannya adalah $x>5$.
Kasus 2: $5-x\ge 0⟺x\le 5$
Oleh karena $x\ge 5$, maka kedua ruas padapertidaksamaan $\sqrt{x-3}>5-x$ bernilai non-negatif sehingga dapat dikuadratkan.
$\begin{array}{cc}(\sqrt{x-3}{)}^2& >(5-x{)}^2\\ x-3& >25-10x+x^2\\ x^2-11x+28& <0\\ (x-4)(x-7)& <0\end{array}$
Pembuat nol: $x=4$ atau $x=7$.
Penyelesaian: $4<x<7$.
Syarat akar:
$x-3\ge 0\iff x\ge 3$.
Irisan dari $x\le 5,4<x<7$, dan $x\ge 3$direpresentasikan oleh garis bilangan berikut.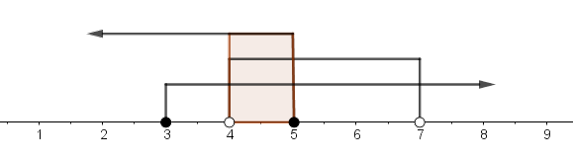
Gabungan penyelesaian dari kedua kasus di atas merupakan nilai-nilai $x$ yang memenuhi pertidaksamaan tersebut, yaitu $\{x|x>4\}$
(Jawaban D)